Aho-Corasick automaton，该算法在1975年产生于贝尔实验室，是著名的多模匹配算法。

前言

ZR的rxd老师加大力度讲了一发AC自动机,凭借着KMP自动机没有自闭的光环,我居然没有自闭!

在晚上自习时重新看了一遍黄队的博客并做了几道题之后,我对AC自动机有了更深的了解,所以来这里瞎扯几句,以便之后复习.

参考资料

前置知识

Trie树(字典树~~不知为啥rxd叫他字母树~~)
KMP单字符串匹配算法

很多神仙都说过一个公式:

Aho-Corasick automaton = Trie + KMP

没错,AC自动机正是以Trie的结构为基础结合KMP的思想建立的。

建立

AC自动机是一个用来求解多模式串匹配问题的算法.

建立一个AC自动机通常需要两步:

一棵Trie的结构,把所有的模式串插入Trie
KMP单字符串匹配算法的思想,对Trie上的节点建立失配指针

Trie构建

和普通的Trie没有什么区别…,直接写一个Trie的Insert操作即可.

注意:这里Trie上的每一个节点是一个模式串的前缀.为了简便,我们将在下文把他称为一个状态(此处借用OI-wiki的约定),Trie的每一个节点表示一个状态,Trie的边可以看作状态的转移(~~这怎么有点像dp~~)

我们把所有这些状态组成的集合称为$U$

因为我们只利用字典树的结构,所以只用把模式串插入Trie即可.

构造失配指针

AC自动机利用一个失配指针failed来辅助匹配

状态(节点)u的failed指针指向状态v,且$v \in U$,并且v是u的最长后缀.

注意:这里的failed和KMP算法中的next指针的不同点在于next指针求的是最长的Border(也就是最长前后缀),而failed是最长后缀.

清楚不同点之后,我们利用KMP的思想来构建failed指针:

我们通过一遍BFS来构建,假设现在我们BFS到的节点为now,他的父亲为fa,fa通过字符str转移到now上,即Trie[fa][str] = now.

由于这是BFS,那么深度小于now的failed指针都已经被求出(这自然包括fa)

我们首先查询fa的failed指针:

如果Trie[failed[fa]][str]指向的值w存在,那么我们就让failed[now] = w.
如果上式并不存在,那么我们继续跳failed,即找到failed[failed[p]],如果还是不存在,那么继续跳,直到找到满足的状态为止.
如果跳到根节点也没有找到,那么直接令failed[now]等于根节点

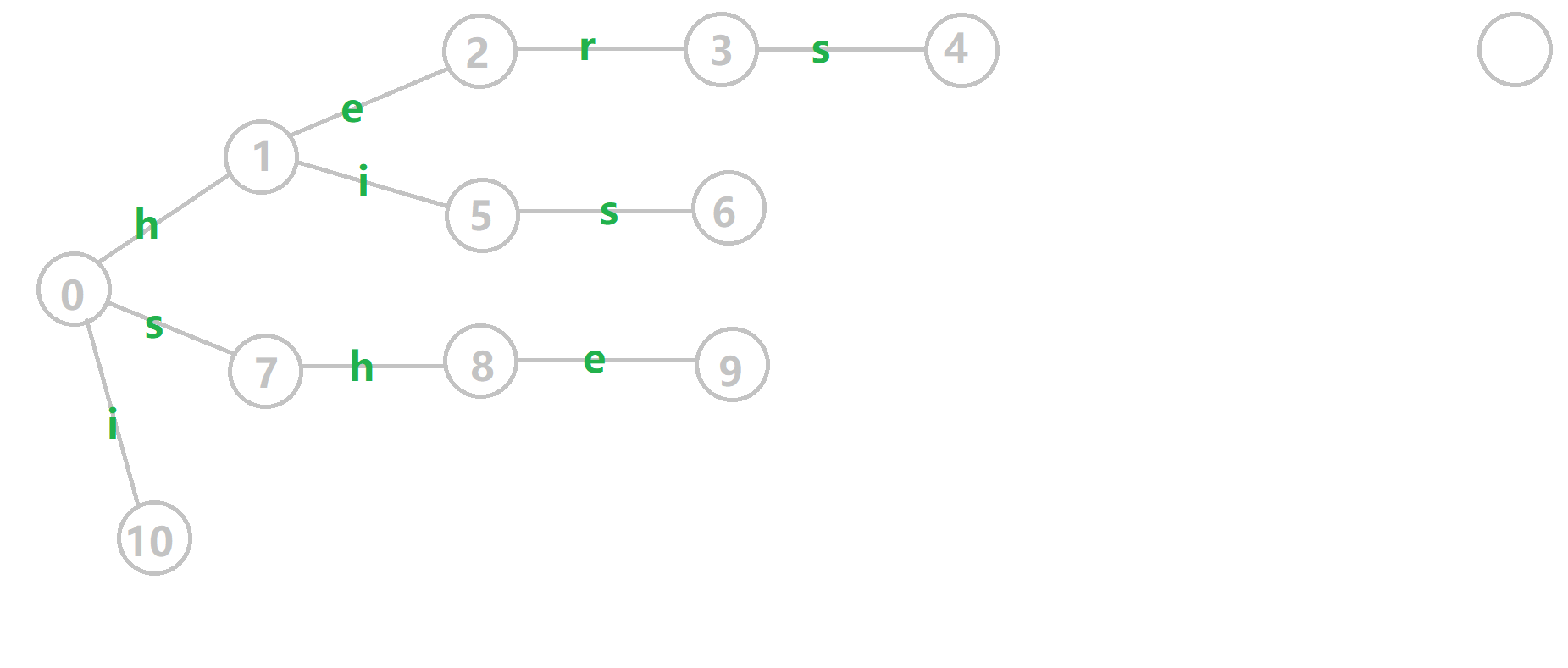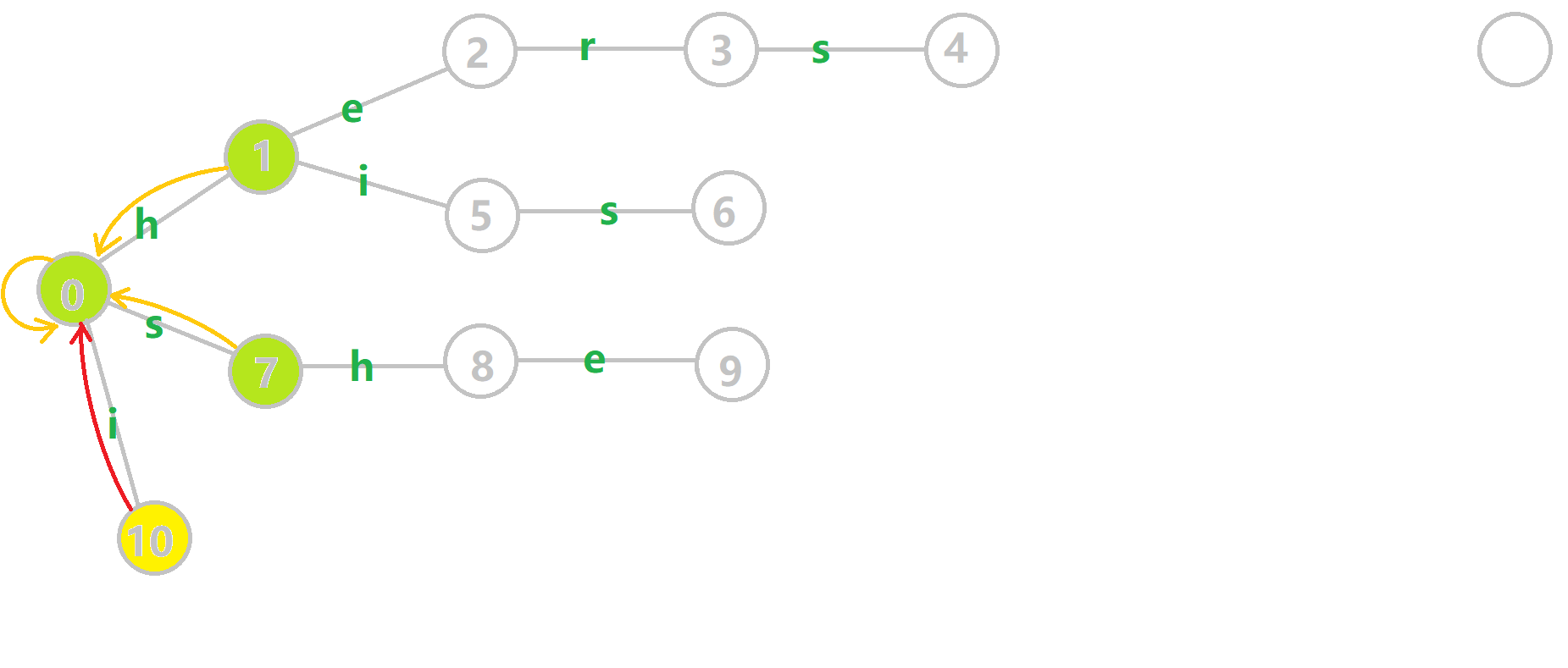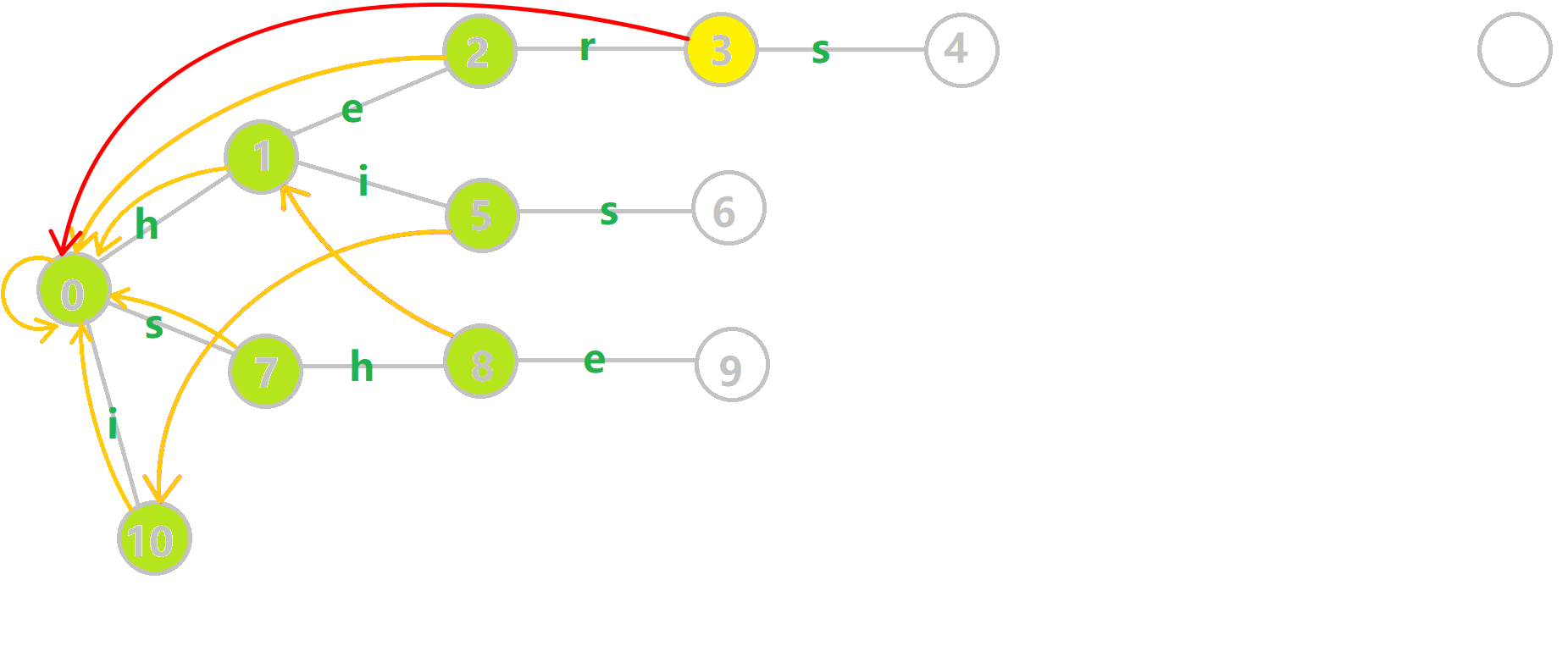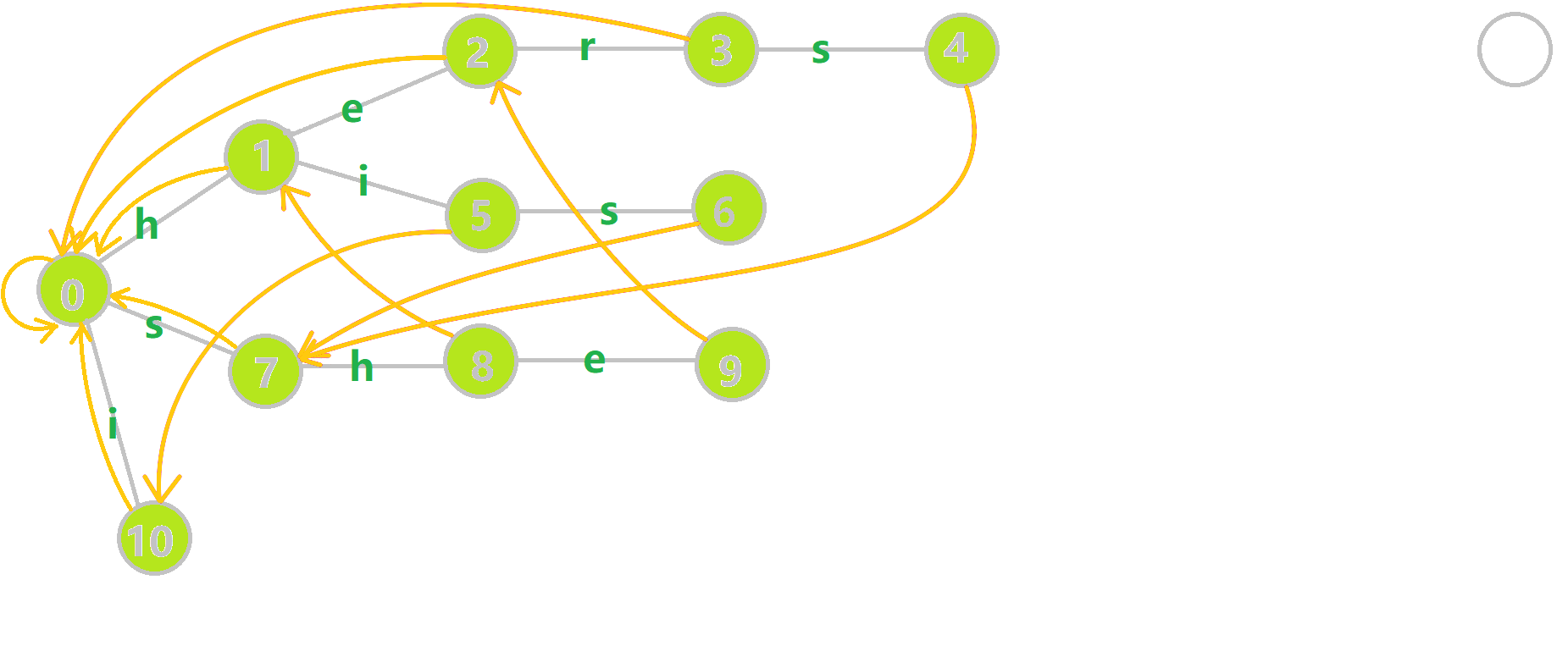
这里有一张来自OI-wiki的gif,帮助大家理解.

Trie图与AC自动机的优化

我们发现,在上述过程中的暴力跳failed这一段时间复杂度不太优秀,那么我们引入Trie图来优化.

我们考虑在当前节点的父亲的failed指针无法通过str字符进行转移的情况下,可以通过修改Trie树的结构来压缩状态.

我们考虑状态u,如果在u后面加上一个字符str向下转移成下一个状态v(我们记这个东西为u' = trans(u,str)).

如果v存在,那么一定有一个模式串的前缀为v.
如果v不存在,那么我们让trans(u,str)指向trans(failed[u],str)
对于上一个东西的解释:因为failed[u]是状态u的后缀,那么显然trans(failed[u],str)就是u'的后缀

这里还是有一张来自OI-wiki的gif,帮助大家理解

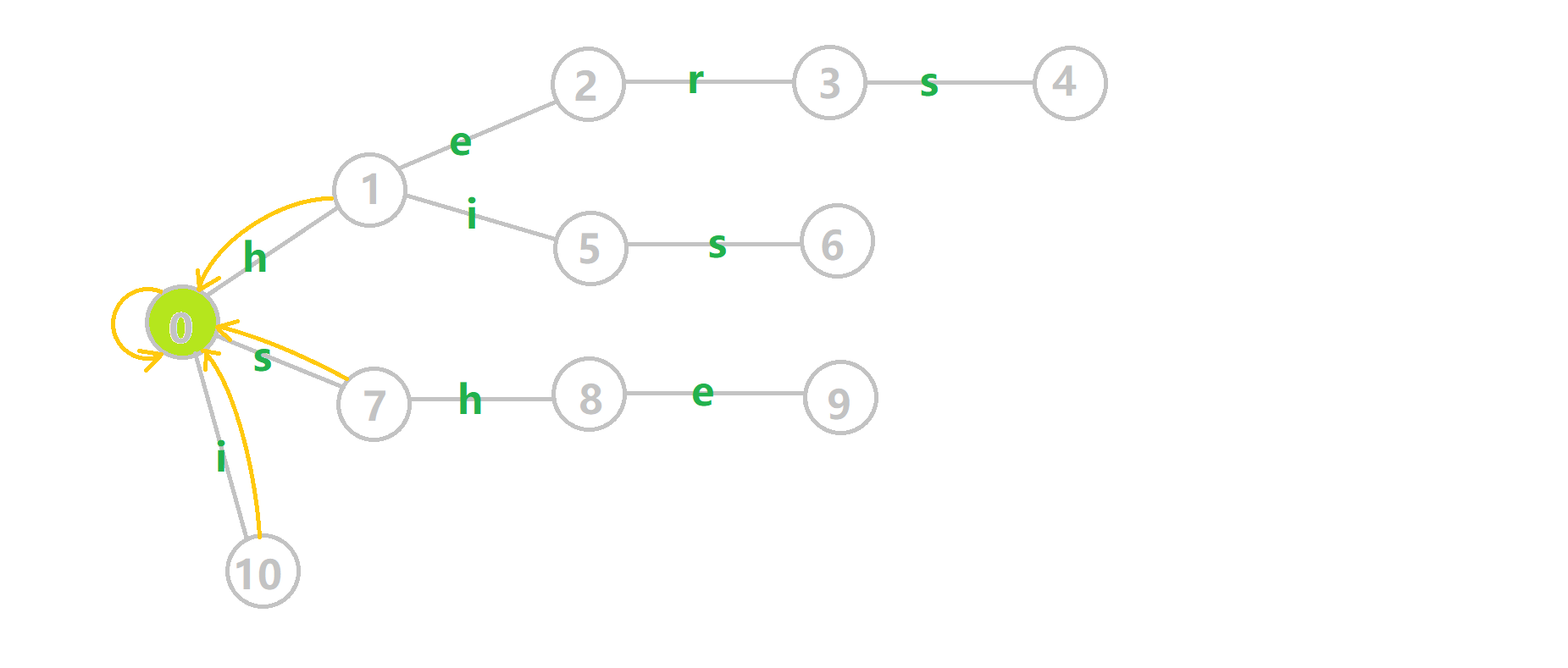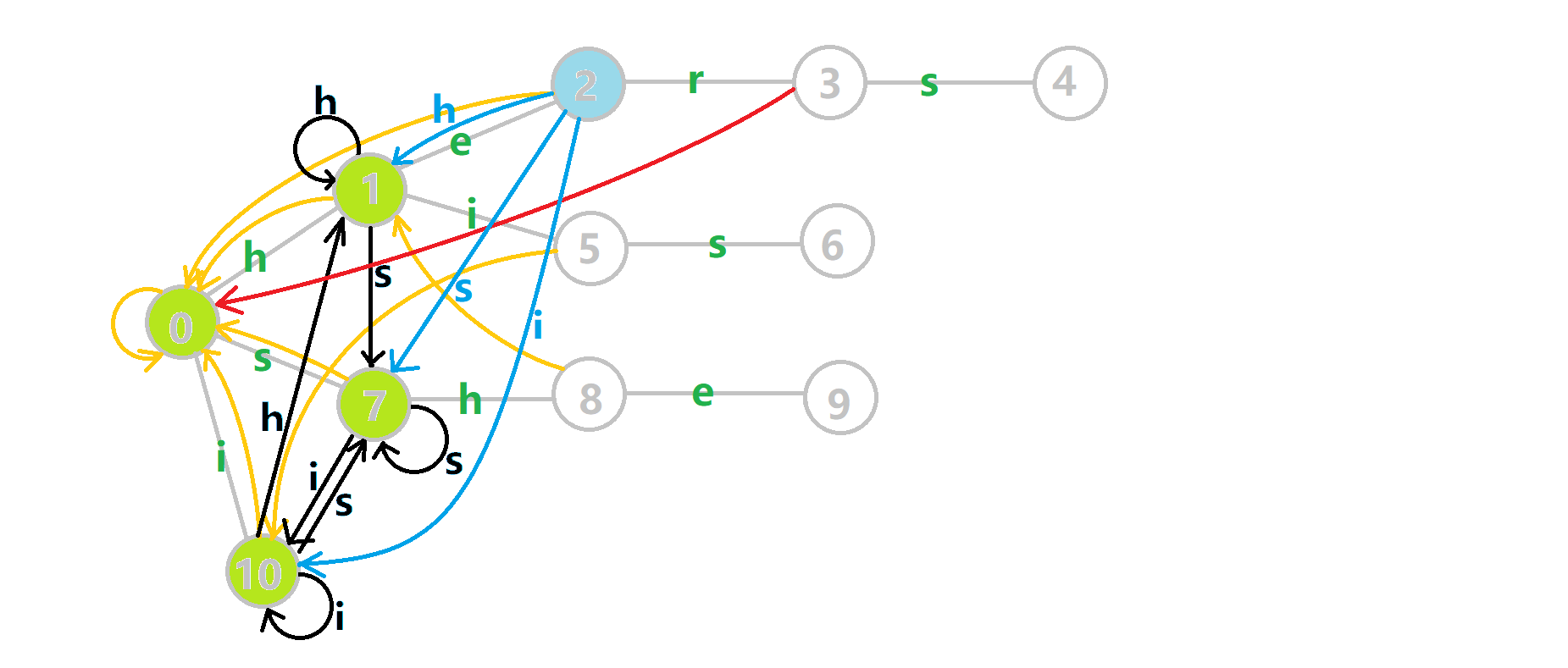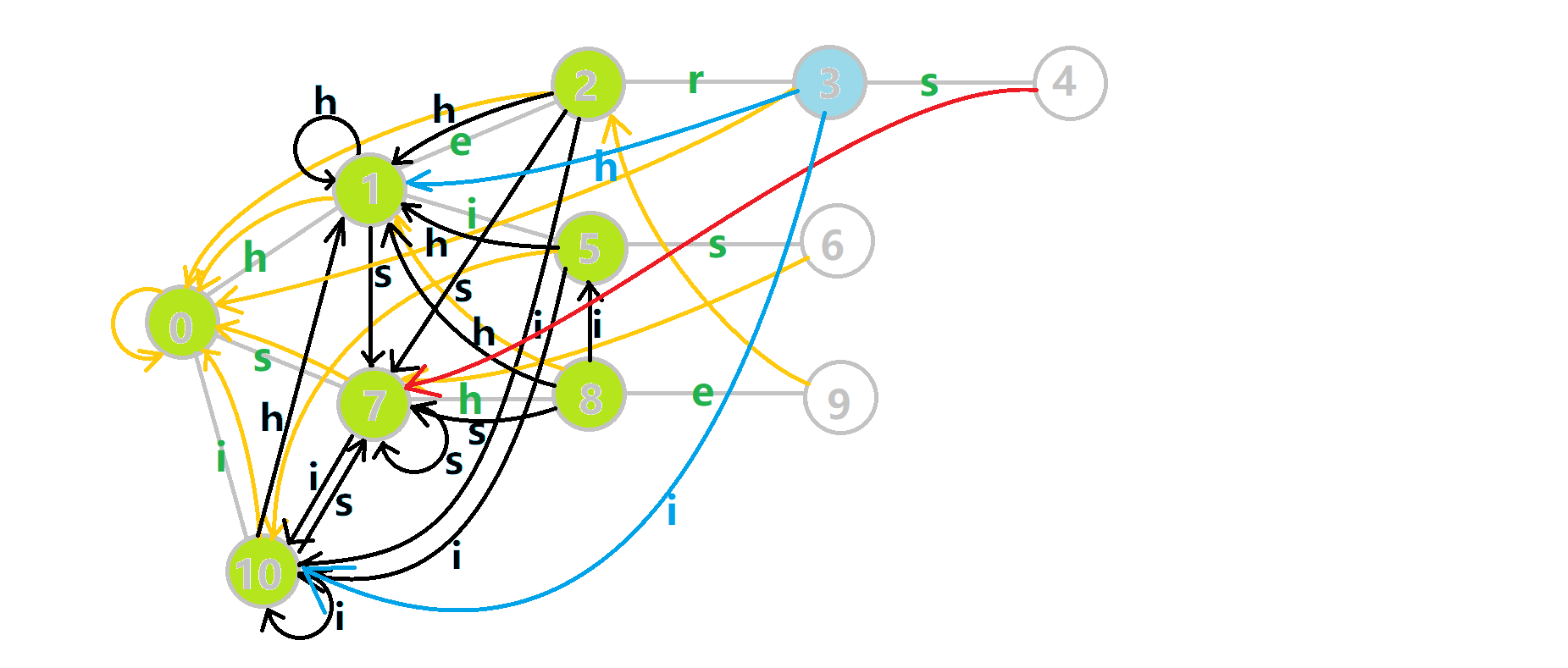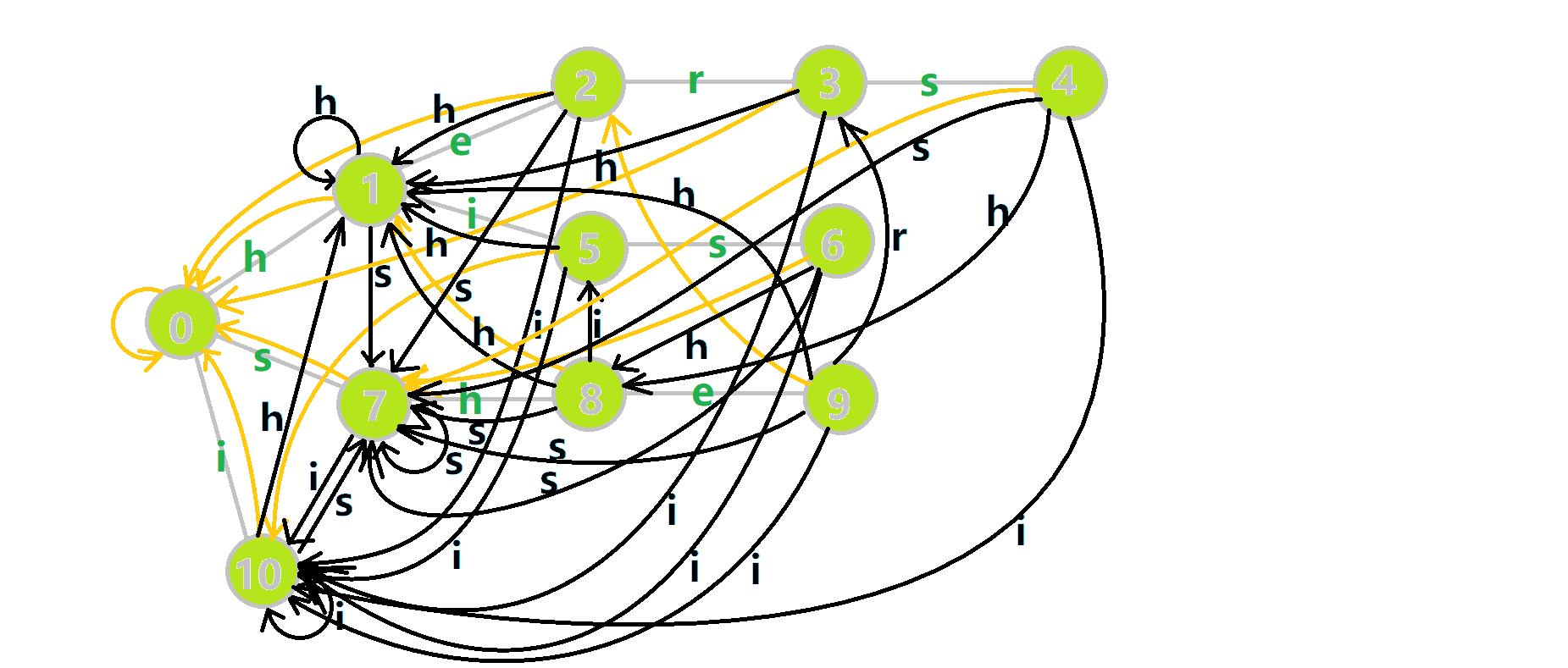
可以发现,这些黑色的边将Trie树变成了Trie图,通过压缩状态简化了跳failed的时间

时间复杂度

AC 自动机的时间复杂度在需要找到所有匹配位置时是$O(|s|+m)$, $|s|$是文本串长度,$m$表示模板串的总匹配次数；

实现

我们以LuoguP3808为例.

// luogu-judger-enable-o2
/* Headers */
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cctype>
#include<algorithm>
#include<vector>
#include<queue>
#include<stack>
#include<climits>
#include<iostream>
#include<map>
#define FOR(i,a,b,c) for(int i=(a);i<=(b);i+=(c))
#define ROF(i,a,b,c) for(int i=(a);i>=(b);i-=(c))
#define FORL(i,a,b,c) for(long long i=(a);i<=(b);i+=(c))
#define ROFL(i,a,b,c) for(long long i=(a);i>=(b);i-=(c))
#define FORR(i,a,b,c) for(register int i=(a);i<=(b);i+=(c))
#define ROFR(i,a,b,c) for(register int i=(a);i>=(b);i-=(c))
#define lowbit(x) x&(-x)
#define LeftChild(x) x<<1
#define RightChild(x) (x<<1)+1
#define RevEdge(x) x^1
#define FILE_IN(x) freopen(x,"r",stdin);
#define FILE_OUT(x) freopen(x,"w",stdout);
#define CLOSE_IN() fclose(stdin);
#define CLOSE_OUT() fclose(stdout);
#define IOS(x) std::ios::sync_with_stdio(x)
#define Dividing() printf("-----------------------------------\n");
namespace FastIO{
    const int BUFSIZE = 1 << 20;
    char ibuf[BUFSIZE],*is = ibuf,*its = ibuf;
    char obuf[BUFSIZE],*os = obuf,*ot = obuf + BUFSIZE;
    inline char getch(){
        if(is == its)
            its = (is = ibuf)+fread(ibuf,1,BUFSIZE,stdin);
        return (is == its)?EOF:*is++;
    }
    inline int getint(){
        int res = 0,neg = 0,ch = getch();
        while(!(isdigit(ch) || ch == '-') && ch != EOF)
            ch = getch();
        if(ch == '-'){
            neg = 1;ch = getch();
        }
        while(isdigit(ch)){
            res = (res << 3) + (res << 1)+ (ch - '0');
            ch = getch();
        }
        return neg?-res:res;
    }
    inline void flush(){
        fwrite(obuf,1,os-obuf,stdout);
        os = obuf;
    }
    inline void putch(char ch){
        *os++ = ch;
        if(os == ot)	flush();
    }
    inline void putint(int res){
        static char q[10];
        if(res==0)	putch('0');
        else if(res < 0){putch('-');res = -res;}
        int top = 0;
        while(res){
            q[top++] = res % 10 + '0';
            res /= 10;
        }
        while(top--)	putch(q[top]);
    }
    inline void space(bool x){
    	if(!x) putch('\n');
    	else putch(' ');
    }
}
inline void read(int &x){
    int rt = FastIO::getint();
    x = rt;
}
inline void print(int x,bool enter){
    FastIO::putint(x);
    FastIO::flush();
    FastIO::space(enter);
}
/* definitions */
/* functions */
namespace Solution{
    const int MAXN = 5e5 + 10;
    const int MAXM = 1e6 + 10;
    std::queue<int> Q;
    int n;
    struct AhoCorasickAutomaton{
        int str[MAXN][26],val[MAXN],failed[MAXN],cnt;
        inline void Insert(char *s){
            int len = strlen(s), now = 0;
            FOR(i,0,len-1,1){
                int value = s[i] - 'a';
                if(!str[now][value]) str[now][value] = ++cnt;
                now = str[now][value];
            }
            val[now]++;
        }
        inline void BFS_Failed(){
            FOR(i,0,25,1) if(str[0][i]) failed[str[0][i]] = 0, Q.push(str[0][i]);
            while(!Q.empty()){
                int first = Q.front(); Q.pop();
                FOR(i,0,25,1)
                    if(str[first][i]) failed[str[first][i]] = str[failed[first]][i], Q.push(str[first][i]);
                    else str[first][i] = str[failed[first]][i];
             }
        }
        inline int Query(char *s){
            int len = strlen(s), now = 0, ans = 0;
            FOR(i,0,len-1,1){
                now = str[now][s[i] - 'a'];
                for(int k = now; k && ~val[k];k=failed[k]) ans += val[k], val[k] = -1;
            }
            return ans;
        }
    };
    AhoCorasickAutomaton AC;
    char ch[MAXM];
    inline void solve(){
        scanf("%d",&n);
        FOR(i,1,n,1) scanf("%s",ch), AC.Insert(ch);
        AC.BFS_Failed();
        scanf("%s",ch); int ans = AC.Query(ch);
        printf("%d\n",ans);
    }
}
int main(int argc,char *argv[]){
    Solution::solve();
    return 0;
}

AC自动机学习笔记

前言