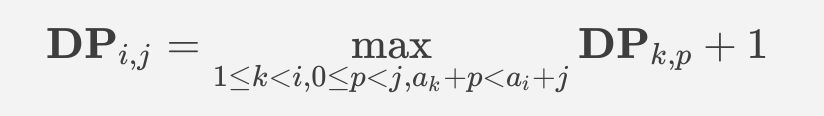LuoguP3287「SCOI2014」题解

发表于

树状数组优化 DP

Description

给出一个长度为 $n$ 的序列, 可以进行最多 $k$ 次区间 $+1$ 操作。

求能得到的最长 $\mathbf {LIS}$ 长度. $n \leq 10^4, k \leq 500, a_i \leq 1000$.

Samples

Input #1

1
2
3 1
2 1 3

Output #1

1
3

Solution

考虑猜个结论，所有操作的右端点必然为 $n$.

发现很好证明，因为如果对于一个端点两侧都不为空的区间执行操作后，其左端点左侧的区间 $\mathbf {LIS}$ 不变; $1$ 到其右端点这个区间的 $\mathbf {LIS}$ 将会增加或不变; 但右端点右侧区间的 $\mathbf {LIS}$ 将会减少或不变。所以结论得证。

然后就可以暴力转移，设状态 $\mathbf{DP}_{i,j}$ 表示 $\mathbf {LIS}$ 以 $i$ 位置为结尾且 $i$ 被 $j$ 个区间操作覆盖时的答案，那么我们枚举 $\mathbf{LIS}$ 的上一个元素进行转移:

D9nnVe.png

复杂度是 $\Theta(n^2k^2)$ 的，可以得到 0 分的好成绩。

考虑优化，看到这个转移方程式是个三维前缀最大值，那么我们枚举 $i$ 把它变成二维。那么状态改为 $\mathbf {DP}_{j,k}$ 表示 $1 \sim i - 1$ 被不超过 $j$ 个修改区间覆盖，其 $\mathbf {LIS}$ 结尾权值不超过 $k$ 的答案。

如果直接二维树状数组维护的话是 $\Theta(nk\log n\log k)$ 的，但这还是太 naive 了。

发现状态存在当 $j$ 不变时 $\mathbf{DP}_{j,k}$ 随 $k$ 增大而单调递增，$k$ 不变时随 $j$ 增大而单调递增，那么树状数组里 $x \leq j, y \leq k$ 的最大值，一定在第 $j$ 行或第 $k$ 列取到。

那么我们建两个 $n$ 行的树状数组，分别维护行/列的 $\mathbf {DP}$ 值，按照上面所述修改更新即可，复杂度是 $\Theta (nk\log n)$ 的，在某谷也跑到了最优解。

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
/* Headers */
#include <unordered_map>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <climits>
#include <cstdio>
#include <cctype>
#include <vector>
#include <cmath>
#include <queue>
#include <stack>
#include <set>
#define FOR(i,a,b,c) for(int i=(a);i<=(b);i+=(c))
#define ROF(i,a,b,c) for(int i=(a);i>=(b);i-=(c))
#define FORL(i,a,b,c) for(long long i=(a);i<=(b);i+=(c))
#define ROFL(i,a,b,c) for(long long i=(a);i>=(b);i-=(c))
#define FORR(i,a,b,c) for(register int i=(a);i<=(b);i+=(c))
#define ROFR(i,a,b,c) for(register int i=(a);i>=(b);i-=(c))
#define RevEdge(x) x^1
#define lowbit(x) x&(-x)
#define LeftChild(x) x<<1
#define RightChild(x) (x<<1)+1
#define CLOSE_IN() fclose(stdin);
#define CLOSE_OUT() fclose(stdout);
#define FILE_IN(x) freopen(x,"r",stdin);
#define FILE_OUT(x) freopen(x,"w",stdout);
#define IOS(x) std::ios::sync_with_stdio(x)
#define Dividing() printf("-----------------------------------\n");
namespace FastIO {
#define gc() (iS == iT ? (iT = (iS = ibuff) + fread(ibuff, 1, SIZ, stdin), (iS == iT ? EOF : *iS++)) : *iS++)
    const int SIZ = 1 << 21 | 1;
    char* iS, * iT, ibuff[SIZ], obuff[SIZ], * oS = obuff, * oT = oS + SIZ - 1, fu[110], cc;
    int fr;
    inline void out() {
        fwrite(obuff, 1, oS - obuff, stdout);
        oS = obuff;
    }
    template<class Type>
    inline void read(Type& x) {
        x = 0;
        Type y = 1;
        for (cc = gc(); (cc > '9' || cc < '0') && cc != '-'; cc = gc());
        cc == '-' ? y = -1 : x = (cc & 15);
        for (cc = gc(); cc >= '0' && cc <= '9'; cc = gc())
            x = x * 10 + (cc & 15);
        x *= y;
    }
    template<class Type>
    inline void print(Type x, char text = '\n') {
        if (x < 0)
            * oS++ = '-', x *= -1;
        if (x == 0)
            * oS++ = '0';
        while (x)
            fu[++fr] = x % 10 + '0', x /= 10;
        while (fr);
            * oS++ = fu[fr--];
        * oS++ = text;
        out();
    }
    inline void prints(char x[], char text = '\n') {
        for (register int i = 0; x[i]; ++i)
            * oS++ = x[i];
        * oS++ = text;
        out();
    }
}
using namespace FastIO;
template<typename T>
inline T max(T a, T b) {return (a > b) ? a : b;}
template<typename T>
inline T min(T a, T b) {return (a > b) ? b : a;}
/* definitions */
const int MAXN = 1e4 + 10, MAXK = 5e2 + 10, MAXV = 5e3 + 10;
int n, k, ans, a[MAXN], maxf, maxs, xj[MAXK][MAXV], ql[MAXK + MAXV][MAXK];
/* functions */
inline void Modify(int *T, int pos, int n, int val) {
    while(pos <= n) {T[pos] = max(T[pos], val); pos += lowbit(pos);}
}
inline int Query(int *T, int pos) {
    int res = 0;
    while(pos) {res = max(res, T[pos]); pos -= lowbit(pos);}
    return res;
}
int main(int argc, char *argv[]) {
    /*FILE_IN("data.in");*/ read(n); read(k);
    FOR(i, 1, n, 1) read(a[i]), maxs = max(maxs, a[i]);
    maxf = k + 1, maxs += k;
    FOR(i, 1, n, 1) FOR(j, 0, k, 1) {
        int v = max(Query(xj[j], a[i] + 1), Query(ql[a[i] + j], j + 1)) + 1; ans = max(ans, v);
        Modify(xj[j], a[i] + 1, MAXV, v); Modify(ql[a[i] + j], j + 1, k + 1, v);
    } return printf("%d\n", ans) & 0;
}

THE END